Tumbling Mill (Power, Morrell Continuum): Difference between revisions

From Met Dynamics
Jump to navigation Jump to search
m (1 revision imported)
imported>Scott.Munro
mNo edit summary
 
(2 intermediate revisions by 2 users not shown)
Line 7: Line 7:
== Model theory ==
== Model theory ==


{{Restricted content}}
<hide>
Morrell's Continuum approach expresses power input to the motor of a tumbling mill as:{{Morrell (1996a)}}
Morrell's Continuum approach expresses power input to the motor of a tumbling mill as:{{Morrell (1996a)}}


Line 27: Line 30:
The net power imparted to the charge in the cylindrical section of the mill was analytically derived as:
The net power imparted to the charge in the cylindrical section of the mill was analytically derived as:


:<math>P_{\rm t} = \frac{\pi g L N_{\rm m} r_{\rm m}}{3 \left (r_{\rm m} - zr_i \right )} \left [ 2r_{\rm m}^3 - 3zr_{\rm m}^2 + r_i^3 \left (3z - 2 \right ) \right ] \times \big [ \rho_{\rm c} \left ( \sin \theta_{\rm S} - \sin \theta_{\rm T} \right ) + \rho_{\rm p} \left ( \sin \theta_{\rm T} - \sin \theta_{\rm TO} \big ) \right ] + L \rho_{\rm c} \left ( \frac{N_{\rm m}r_{\rm m} \pi}{\left ( r_{\rm m} - zr_i \right)} \right ) \left [ \left( r_{\rm m} - zr_i \right )^4 - r_i^4 \left (z - 1 \right )^4 \right ] </math>
:<math>P_{\rm t} = \frac{\pi g L N_{\rm m} r_{\rm m}}{3 \left (r_{\rm m} - zr_{\rm i} \right )} \left [ 2r_{\rm m}^3 - 3zr_{\rm m}^2 + r_{\rm i}^3 \left (3z - 2 \right ) \right ] \times \big [ \rho_{\rm c} \left ( \sin \theta_{\rm S} - \sin \theta_{\rm T} \right ) + \rho_{\rm p} \left ( \sin \theta_{\rm T} - \sin \theta_{\rm TO} \big ) \right ] + L \rho_{\rm c} \left ( \frac{N_{\rm m}r_{\rm m} \pi}{\left ( r_{\rm m} - zr_{\rm i} \right)} \right ) \left [ \left( r_{\rm m} - zr_{\rm i} \right )^4 - r_{\rm i}^4 \left (z - 1 \right )^4 \right ] </math>


and for the cone end section:
and for the cone end section:


:<math>P_{\rm c} = \frac{\pi L_{\rm d} g N_{\rm m}}{3(r_{\rm m} - r_{\rm t})} \bigg \{ \left ( r_{\rm m}^4 - 4r_{\rm m}r_i^3 + 3r_i^4 \right ) \big[ \rho_{\rm c} \left ( \sin \theta_{\rm S} - \sin \theta_{\rm T} \right ) + \rho_{\rm p} \left ( \sin \theta_{\rm T} - \sin \theta_{\rm TO} \right ) \big] \bigg \} + \frac{2 \pi^3 N_{\rm m}^3 L_{\rm d} \rho_{\rm c}}{5(r_{\rm m} - r_{\rm t})} \big ( r_{\rm m}^5 - 5r_{\rm m}r_i^4 + 4r_i^5 \big )</math>
:<math>P_{\rm c} = \frac{\pi L_{\rm d} g N_{\rm m}}{3(r_{\rm m} - r_{\rm t})} \bigg \{ \left ( r_{\rm m}^4 - 4r_{\rm m}r_{\rm i}^3 + 3r_{\rm i}^4 \right ) \big[ \rho_{\rm c} \left ( \sin \theta_{\rm S} - \sin \theta_{\rm T} \right ) + \rho_{\rm p} \left ( \sin \theta_{\rm T} - \sin \theta_{\rm TO} \right ) \big] \bigg \} + \frac{2 \pi^3 N_{\rm m}^3 L_{\rm d} \rho_{\rm c}}{5(r_{\rm m} - r_{\rm t})} \big ( r_{\rm m}^5 - 5r_{\rm m}r_{\rm i}^4 + 4r_{\rm i}^5 \big )</math>


where:
where:
Line 44: Line 47:
* <math>r_{\rm m}</math> is the mill radius inside liners (m)
* <math>r_{\rm m}</math> is the mill radius inside liners (m)
* <math>r_{\rm t}</math> is the trunnion radius inside liners (m)
* <math>r_{\rm t}</math> is the trunnion radius inside liners (m)
* <math>r_i</math> is the inner charge surface radius (m)
* <math>r_{\rm i}</math> is the inner charge surface radius (m)
* <math>\theta_{\rm S}</math> is the angle of the charge shoulder (radians)
* <math>\theta_{\rm S}</math> is the angle of the charge shoulder (radians)
* <math>\theta_{\rm T}</math> is the angle of the charge toe (radians)
* <math>\theta_{\rm T}</math> is the angle of the charge toe (radians)
Line 71: Line 74:
=== Charge position ===
=== Charge position ===


The charge motion power equations require the position of the charge shoulder (<math>\theta_{\rm S}</math>), charge toe (<math>\theta_{\rm T}</math>), slurry pool level (<math>\theta_{\rm TO}</math>, for overflow discharge mills) and the inner charge surface radius (<math>r_i</math>), in addition to mill dimensions and charge composition.  
The charge motion power equations require the position of the charge shoulder (<math>\theta_{\rm S}</math>), charge toe (<math>\theta_{\rm T}</math>), slurry pool level (<math>\theta_{\rm TO}</math>, for overflow discharge mills) and the inner charge surface radius (<math>r_{\rm i}</math>), in addition to mill dimensions and charge composition.  


Morrell developed the following series of relations to estimate the charge geometry.{{Morrell (1996a)}}
Morrell developed the following series of relations to estimate the charge geometry.{{Morrell (1996a)}}
Line 103: Line 106:
where <math>r_{\rm t}</math> (m) is the radius of the trunnion.
where <math>r_{\rm t}</math> (m) is the radius of the trunnion.


The inner '''charge surface radius''', <math>r_i</math> (m), is:
The inner '''charge surface radius''', <math>r_{\rm i}</math> (m), is:


:<math>r_i = r_{\rm m} \left ( 1 - \frac{2 \pi \beta J_{\rm t}}{2 \pi + \theta_{\rm S} - \theta_{\rm T}} \right )^{0.5}</math>
:<math>r_{\rm i} = r_{\rm m} \left ( 1 - \frac{2 \pi \beta J_{\rm t}}{2 \pi + \theta_{\rm S} - \theta_{\rm T}} \right )^{0.5}</math>


where the fraction of total charge in the active region, <math>\beta</math> (frac), is:
where the fraction of total charge in the active region, <math>\beta</math> (frac), is:
Line 147: Line 150:
where <math>D</math> is mill diameter inside liners (m)
where <math>D</math> is mill diameter inside liners (m)


== Additional notes==
=== Additional notes ===


The Morrell C model is only applicable to grate discharge mills that do not exhibit a slurry pool, i.e. <math>U \leq 1</math>.
The Morrell C model is only applicable to grate discharge mills that do not exhibit a slurry pool, i.e. <math>U \leq 1</math>.


For overflow discharge mills, the slurry pool component is accounted for by the <math>\theta_{\rm TO}</math> term, which assumes overflow at the exact height of the trunnion lip.
For overflow discharge mills, the slurry pool component is accounted for by the <math>\theta_{\rm TO}</math> term, which assumes overflow at the exact height of the trunnion lip.
</hide>


== Excel ==
== Excel ==
Line 193: Line 197:
\theta_{\rm T} \text{ (rad)}\\
\theta_{\rm T} \text{ (rad)}\\
\theta_{\rm TO} \text{ (rad)}\\
\theta_{\rm TO} \text{ (rad)}\\
r_i\text{ (m)}\\
r_{\rm i}\text{ (m)}\\
\end{bmatrix}\;\;\;\;\;\;
\end{bmatrix}\;\;\;\;\;\;
</math>
</math>

Latest revision as of 11:13, 4 December 2024

Description

This article describes the Morrell Continuum (Morrell C) method for estimating the power draw of a tumbling mill.[1]

The Morrell C model is a theoretical approach based on the dynamics of the grinding charge. By making simplifying assumptions about the charge shape, composition and position, Morrell developed analytical solutions to equations describing the the rate at which potential and kinetic energy is imparted to the charge during mill rotation.

Model theory

Nuvola apps important blue.svg.png This content is available to registered users. Please log in to view.

Excel

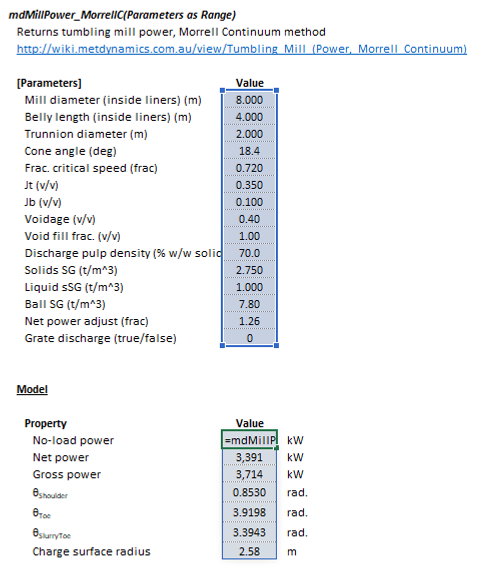
The Morrell Continuum mill power model may be invoked from the Excel formula bar with the following function call: 

=mdMillPower_MorrellC(Parameters as Range)

Invoking the function with no arguments will print Help text associated with the model, including a link to this page.

The Parameters array and model results are defined below in matrix notation, along with an example image showing the selection of the same arrays in the Excel interface:


where:

  • is the diameter of the discharge trunnion (m)
  • is the mass fraction of solids in the discharge pulp (% w/w)
  • is the density of liquids (t/m3)
  • is true if the mill is configured with a grate discharge, false if an overflow discharge
Figure 3. Example showing the selection of the Parameters (blue frame), and Results (light blue frame) arrays in Excel.

SysCAD

The Morrell Continuum power model is an optional calculation for tumbling mill units. If selected, the input and display parameters below are shown.

Tag (Long/Short) Input / Display Description/Calculated Variables/Options
MorrellC
HelpLink ButtonModelHelp.png Opens a link to this page using the system default web browser. Note: Internet access is required.
MillDiameter Input/Display Diameter of the mill (inside liners).
BellyLength Input/Display Length of the cylindrical section (belly) of the mill (inside liners).
TrunnionDiameter Input/Display Diameter of the trunnion (inside liners).
FracCS Input/Display Fraction critical speed of the mill.
Jt Input/Display Volumetric fraction of the mill occupied by balls and coarse rock (including voids).
Jb Input/Display Volumetric fraction of the mill occupied by balls (including voids).
Voidage Input/Display Volumetric fraction of interstitial void space in the charge. Usually 0.4.
VoidFillFraction Input/Display Volumetric fraction of interstitial grinding media voidage occupied by slurry.
ConeAngle Input/Display Angular displacement of the cone surface from the vertical direction.
DischargePulpDensity Display Mass fraction of solids in discharge slurry.
SolidsSG Display Specific Gravity or density of solids.
LiquidsSG Display Specific Gravity or density of liquids.
BallSG Input/Display Specific Gravity or density of balls.
DischargeType Grate/Overflow Discharge configuration, grate or overflow.
NetPowerAdjust Input Lumped calibration parameter accounting for power losses. Found to be a value of 1.26 for industrial mills.
ThetaShoulder Display Angle of the charge shoulder.
ThetaToe Display Angle of the charge toe.
ThetaSlurryToe Display Angle of the slurry pool surface at the toe.
ChargeSurfaceRadius Display Radius of the inner surface of the charge.
NoLoadPower Display Power input to the motor when the mill is empty (no balls, rocks or slurry).
NetPower Display Charge motion power, including losses.
GrossPower Display Power input to the motor.

See also

References

  1. ↑ Morrell, S., 1996. Power draw of wet tumbling mills and its relationship to charge dynamics. Pt. 1: a continuum approach to mathematical modelling of mill power draw. Transactions of the Institution of Mining and Metallurgy. Section C. Mineral Processing and Extractive Metallurgy, 105.
Retrieved from "https://wiki.metdynamics.com.au/index.php?title=Tumbling_Mill_(Power,_Morrell_Continuum)&oldid=2208"