Tumbling Mill (Power, Morrell Continuum): Difference between revisions
Jump to navigation
Jump to search
md>Scott.Munro m (Text replacement - "\theta_{T}" to "\theta_{\rm T}") |
imported>Scott.Munro mNo edit summary |
||
| (3 intermediate revisions by 2 users not shown) | |||
| Line 7: | Line 7: | ||
== Model theory == | == Model theory == | ||
{{Restricted content}} | |||
<hide> | |||
Morrell's Continuum approach expresses power input to the motor of a tumbling mill as:{{Morrell (1996a)}} | Morrell's Continuum approach expresses power input to the motor of a tumbling mill as:{{Morrell (1996a)}} | ||
| Line 27: | Line 30: | ||
The net power imparted to the charge in the cylindrical section of the mill was analytically derived as: | The net power imparted to the charge in the cylindrical section of the mill was analytically derived as: | ||
:<math>P_{\rm t} = \frac{\pi g L N_{\rm m} r_{\rm m}}{3 \left (r_{\rm m} - | :<math>P_{\rm t} = \frac{\pi g L N_{\rm m} r_{\rm m}}{3 \left (r_{\rm m} - zr_{\rm i} \right )} \left [ 2r_{\rm m}^3 - 3zr_{\rm m}^2 + r_{\rm i}^3 \left (3z - 2 \right ) \right ] \times \big [ \rho_{\rm c} \left ( \sin \theta_{\rm S} - \sin \theta_{\rm T} \right ) + \rho_{\rm p} \left ( \sin \theta_{\rm T} - \sin \theta_{\rm TO} \big ) \right ] + L \rho_{\rm c} \left ( \frac{N_{\rm m}r_{\rm m} \pi}{\left ( r_{\rm m} - zr_{\rm i} \right)} \right ) \left [ \left( r_{\rm m} - zr_{\rm i} \right )^4 - r_{\rm i}^4 \left (z - 1 \right )^4 \right ] </math> | ||
and for the cone end section: | and for the cone end section: | ||
:<math>P_{\rm c} = \frac{\pi L_{\rm d} g N_{\rm m}}{3(r_{\rm m} - r_{\rm t})} \bigg \{ \left ( r_{\rm m}^4 - 4r_{\rm m} | :<math>P_{\rm c} = \frac{\pi L_{\rm d} g N_{\rm m}}{3(r_{\rm m} - r_{\rm t})} \bigg \{ \left ( r_{\rm m}^4 - 4r_{\rm m}r_{\rm i}^3 + 3r_{\rm i}^4 \right ) \big[ \rho_{\rm c} \left ( \sin \theta_{\rm S} - \sin \theta_{\rm T} \right ) + \rho_{\rm p} \left ( \sin \theta_{\rm T} - \sin \theta_{\rm TO} \right ) \big] \bigg \} + \frac{2 \pi^3 N_{\rm m}^3 L_{\rm d} \rho_{\rm c}}{5(r_{\rm m} - r_{\rm t})} \big ( r_{\rm m}^5 - 5r_{\rm m}r_{\rm i}^4 + 4r_{\rm i}^5 \big )</math> | ||
where: | where: | ||
| Line 44: | Line 47: | ||
* <math>r_{\rm m}</math> is the mill radius inside liners (m) | * <math>r_{\rm m}</math> is the mill radius inside liners (m) | ||
* <math>r_{\rm t}</math> is the trunnion radius inside liners (m) | * <math>r_{\rm t}</math> is the trunnion radius inside liners (m) | ||
* <math> | * <math>r_{\rm i}</math> is the inner charge surface radius (m) | ||
* <math>\theta_{\rm S}</math> is the angle of the charge shoulder (radians) | * <math>\theta_{\rm S}</math> is the angle of the charge shoulder (radians) | ||
* <math>\theta_{\rm T}</math> is the angle of the charge toe (radians) | * <math>\theta_{\rm T}</math> is the angle of the charge toe (radians) | ||
| Line 71: | Line 74: | ||
=== Charge position === | === Charge position === | ||
The charge motion power equations require the position of the charge shoulder (<math>\theta_{\rm S}</math>), charge toe (<math>\theta_{\rm T}</math>), slurry pool level (<math>\theta_{\rm TO}</math>, for overflow discharge mills) and the inner charge surface radius (<math> | The charge motion power equations require the position of the charge shoulder (<math>\theta_{\rm S}</math>), charge toe (<math>\theta_{\rm T}</math>), slurry pool level (<math>\theta_{\rm TO}</math>, for overflow discharge mills) and the inner charge surface radius (<math>r_{\rm i}</math>), in addition to mill dimensions and charge composition. | ||
Morrell developed the following series of relations to estimate the charge geometry.{{Morrell (1996a)}} | Morrell developed the following series of relations to estimate the charge geometry.{{Morrell (1996a)}} | ||
| Line 103: | Line 106: | ||
where <math>r_{\rm t}</math> (m) is the radius of the trunnion. | where <math>r_{\rm t}</math> (m) is the radius of the trunnion. | ||
The inner '''charge surface radius''', <math> | The inner '''charge surface radius''', <math>r_{\rm i}</math> (m), is: | ||
:<math> | :<math>r_{\rm i} = r_{\rm m} \left ( 1 - \frac{2 \pi \beta J_{\rm t}}{2 \pi + \theta_{\rm S} - \theta_{\rm T}} \right )^{0.5}</math> | ||
where the fraction of total charge in the active region, <math>\beta</math> (frac), is: | where the fraction of total charge in the active region, <math>\beta</math> (frac), is: | ||
| Line 147: | Line 150: | ||
where <math>D</math> is mill diameter inside liners (m) | where <math>D</math> is mill diameter inside liners (m) | ||
== Additional notes== | === Additional notes === | ||
The Morrell C model is only applicable to grate discharge mills that do not exhibit a slurry pool, i.e. <math>U \leq 1</math>. | The Morrell C model is only applicable to grate discharge mills that do not exhibit a slurry pool, i.e. <math>U \leq 1</math>. | ||
For overflow discharge mills, the slurry pool component is accounted for by the <math>\theta_{\rm TO}</math> term, which assumes overflow at the exact height of the trunnion lip. | For overflow discharge mills, the slurry pool component is accounted for by the <math>\theta_{\rm TO}</math> term, which assumes overflow at the exact height of the trunnion lip. | ||
</hide> | |||
== Excel == | == Excel == | ||
| Line 193: | Line 197: | ||
\theta_{\rm T} \text{ (rad)}\\ | \theta_{\rm T} \text{ (rad)}\\ | ||
\theta_{\rm TO} \text{ (rad)}\\ | \theta_{\rm TO} \text{ (rad)}\\ | ||
r_{\rm i}\text{ (m)}\\ | |||
\end{bmatrix}\;\;\;\;\;\; | \end{bmatrix}\;\;\;\;\;\; | ||
</math> | </math> | ||
Latest revision as of 11:13, 4 December 2024
Description
This article describes the Morrell Continuum (Morrell C) method for estimating the power draw of a tumbling mill.[1]
The Morrell C model is a theoretical approach based on the dynamics of the grinding charge. By making simplifying assumptions about the charge shape, composition and position, Morrell developed analytical solutions to equations describing the the rate at which potential and kinetic energy is imparted to the charge during mill rotation.
Model theory
 This content is available to registered users. Please log in to view.
|
Excel
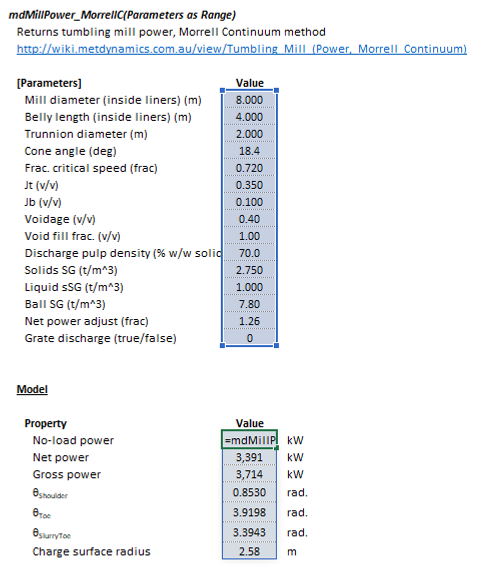
The Morrell Continuum mill power model may be invoked from the Excel formula bar with the following function call:
=mdMillPower_MorrellC(Parameters as Range)
Invoking the function with no arguments will print Help text associated with the model, including a link to this page.
The Parameters array and model results are defined below in matrix notation, along with an example image showing the selection of the same arrays in the Excel interface:
|
|
 Figure 3. Example showing the selection of the Parameters (blue frame), and Results (light blue frame) arrays in Excel. |
SysCAD
The Morrell Continuum power model is an optional calculation for tumbling mill units. If selected, the input and display parameters below are shown.
| Tag (Long/Short) | Input / Display | Description/Calculated Variables/Options |
|---|---|---|
| MorrellC | ||
| HelpLink | 
|
Opens a link to this page using the system default web browser. Note: Internet access is required. |
| MillDiameter | Input/Display | Diameter of the mill (inside liners). |
| BellyLength | Input/Display | Length of the cylindrical section (belly) of the mill (inside liners). |
| TrunnionDiameter | Input/Display | Diameter of the trunnion (inside liners). |
| FracCS | Input/Display | Fraction critical speed of the mill. |
| Jt | Input/Display | Volumetric fraction of the mill occupied by balls and coarse rock (including voids). |
| Jb | Input/Display | Volumetric fraction of the mill occupied by balls (including voids). |
| Voidage | Input/Display | Volumetric fraction of interstitial void space in the charge. Usually 0.4. |
| VoidFillFraction | Input/Display | Volumetric fraction of interstitial grinding media voidage occupied by slurry. |
| ConeAngle | Input/Display | Angular displacement of the cone surface from the vertical direction. |
| DischargePulpDensity | Display | Mass fraction of solids in discharge slurry. |
| SolidsSG | Display | Specific Gravity or density of solids. |
| LiquidsSG | Display | Specific Gravity or density of liquids. |
| BallSG | Input/Display | Specific Gravity or density of balls. |
| DischargeType | Grate/Overflow | Discharge configuration, grate or overflow. |
| NetPowerAdjust | Input | Lumped calibration parameter accounting for power losses. Found to be a value of 1.26 for industrial mills. |
| ThetaShoulder | Display | Angle of the charge shoulder. |
| ThetaToe | Display | Angle of the charge toe. |
| ThetaSlurryToe | Display | Angle of the slurry pool surface at the toe. |
| ChargeSurfaceRadius | Display | Radius of the inner surface of the charge. |
| NoLoadPower | Display | Power input to the motor when the mill is empty (no balls, rocks or slurry). |
| NetPower | Display | Charge motion power, including losses. |
| GrossPower | Display | Power input to the motor. |
See also
References
- ↑ Morrell, S., 1996. Power draw of wet tumbling mills and its relationship to charge dynamics. Pt. 1: a continuum approach to mathematical modelling of mill power draw. Transactions of the Institution of Mining and Metallurgy. Section C. Mineral Processing and Extractive Metallurgy, 105.