Stirred Mill (Perfect Mixing, Dynamic): Difference between revisions
md>Scott.Munro m (→Results) |
imported>Scott.Munro m (→Breakage rate) |
||
| (8 intermediate revisions by 3 users not shown) | |||
| Line 15: | Line 15: | ||
=== Breakage rate === | === Breakage rate === | ||
[[File:StirredMillDimensions1.png|thumb|425px|Figure 2. Schematic of a bottom-fed vertical stirred mill showing key dimensions. The stirrer shown is a screw type with two starts and three turns per start. (After Napier-Munn et al., 1996).{{Napier-Munn et al. (1996)}}]] | [[File:StirredMillDimensions1.png|thumb|425px|Figure 2. Schematic of a bottom-fed, gravity-induced vertical stirred mill showing key dimensions. The stirrer shown is a screw type with two starts and three turns per start. (After Napier-Munn et al., 1996).{{Napier-Munn et al. (1996)}}]] | ||
The breakage function, <math>R_i</math>, is an input parameter for the dynamic Perfect Mixing model, replacing the <math>R_i/D_i</math> term appearing in [[Stirred Mill (Perfect Mixing)#Breakage rate|the steady-state version]]. | The breakage function, <math>R_i</math>, is an input parameter for the dynamic Perfect Mixing model, replacing the <math>R_i/D_i</math> term appearing in [[Stirred Mill (Perfect Mixing)#Breakage rate|the steady-state version]]. | ||
| Line 23: | Line 23: | ||
Adopting the same scaling approach and nomenclature as the [[Ball Mill (Perfect Mixing)|Perfect Mixing ball mill]], the <math>R_i^*</math> rate is scaled by the following relation: | Adopting the same scaling approach and nomenclature as the [[Ball Mill (Perfect Mixing)|Perfect Mixing ball mill]], the <math>R_i^*</math> rate is scaled by the following relation: | ||
:<math>\left(\frac{R}{D^*}\right)_{\rm Sim} = \left(\frac{R}{D^*}\right)_{\rm Orig} \cdot | :<math>\left(\frac{R}{D^*}\right)_{\rm Sim} = \left(\frac{R}{D^*}\right)_{\rm Orig} \cdot f_{\rm Ds} \cdot f_{\rm Hb} \cdot f_{\rm Ns} \cdot f_{\rm S} \cdot f_{\rm T} \cdot f_{\rm Db} \cdot f_{\rm WI}</math> | ||
{{Model theory (Text, Stirred Mill, Perfect Mixing, Breakage Scaling)}} | {{Model theory (Text, Stirred Mill, Perfect Mixing, Breakage Scaling)}} | ||
| Line 41: | Line 41: | ||
=== Internal mesh series === | === Internal mesh series === | ||
{{Model theory (Text, Ball Mill, Perfect Mixing, Internal mesh)}} | {{Model theory (Text, Ball Mill, Perfect Mixing, Internal mesh)|Perfect Mixing}} | ||
=== Multi-component modelling === | === Multi-component modelling === | ||
{{Model theory (Text, Ball Mill, Perfect Mixing, Multi-component)}} | {{Model theory (Text, Ball Mill, Perfect Mixing, Multi-component)|Perfect Mixing|breakage rate}} | ||
=== Slurry filling and discharge === | === Slurry filling and discharge === | ||
| Line 71: | Line 71: | ||
The ''run-to-steady-state'' dynamic Perfect Mixing stirred mill model may be invoked from the Excel formula bar with the following function call: | The ''run-to-steady-state'' dynamic Perfect Mixing stirred mill model may be invoked from the Excel formula bar with the following function call: | ||
<syntaxhighlight lang="vb">=mdUnit_StirredMill_PerfectMixingRiDi(Parameters as Range, Size as Range, MillFeed as Range, OreSG As Range, Appearance as Range, WorkIndexSim as Range, RKnotPositions as Range, RKnotsOrig as Range, Classification as Range)</syntaxhighlight> | <syntaxhighlight lang="vb">=mdUnit_StirredMill_PerfectMixingRiDi(Parameters as Range, Size as Range, MillFeed as Range, OreSG As Range, Appearance as Range, WorkIndexSim as Range, RKnotPositions as Range, RKnotsOrig as Range, Classification as Range, Optional ScalingExponents as Range)</syntaxhighlight> | ||
{{Excel (Text, Help, No Arguments)}} | {{Excel (Text, Help, No Arguments)}} | ||
| Line 95: | Line 95: | ||
S_{\rm Sim}\\ | S_{\rm Sim}\\ | ||
T_{\rm Sim}\\ | T_{\rm Sim}\\ | ||
\ | {\rm WI}_{\rm Orig}\text{ (kWh/t)}\\ | ||
(Q_{\rm M,F})_{\rm L}\text{ (t/h)}\\ | (Q_{\rm M,F})_{\rm L}\text{ (t/h)}\\ | ||
\rho_{\rm L}\text{ (t/m}^{\text{3}}\text{)}\\ | \rho_{\rm L}\text{ (t/m}^{\text{3}}\text{)}\\ | ||
| Line 137: | Line 136: | ||
\end{bmatrix},\;\;\;\;\;\; | \end{bmatrix},\;\;\;\;\;\; | ||
\ | {\rm WI}_{\rm Sim}= \begin{bmatrix} | ||
\ | {\rm WI}_{1}\text{ (kWh/t)} & \dots & {\rm WI}_m\text{ (kWh/t)}\\ | ||
\end{bmatrix},\;\;\;\;\;\; | \end{bmatrix},\;\;\;\;\;\; | ||
| Line 162: | Line 161: | ||
x_{\rm g} & \mbox{if Classification method}=1\mbox{ (Leung)}\\ | x_{\rm g} & \mbox{if Classification method}=1\mbox{ (Leung)}\\ | ||
\end{cases} | \end{cases} | ||
</math> | |||
:<math> | |||
\mathit{ScalingExponents} = \begin{bmatrix} | |||
e_1\\ | |||
e_2\\ | |||
e_3\\ | |||
e_4\\ | |||
e_5\\ | |||
e_6\\ | |||
e_7\\ | |||
\end{bmatrix}^* | |||
</math> | </math> | ||
| Line 177: | Line 188: | ||
* <math>\text{Discharge type}</math> is discharge configuration, ''0 = Overflow discharge at mill height, 1 = Overflow discharge at user-defined slurry filling volume'' | * <math>\text{Discharge type}</math> is discharge configuration, ''0 = Overflow discharge at mill height, 1 = Overflow discharge at user-defined slurry filling volume'' | ||
* <math>\text{User overflow volume}</math> is the user-specified slurry filling volume at which overflow commences (if <math>\text{Discharge type}=1</math>) (m<sup>3</sup>) | * <math>\text{User overflow volume}</math> is the user-specified slurry filling volume at which overflow commences (if <math>\text{Discharge type}=1</math>) (m<sup>3</sup>) | ||
* <math>^*</math> indicates the <math>\mathit{ScalingExponents}</math> array is optional, the default values are used if omitted. | |||
=== Results === | === Results === | ||
| Line 191: | Line 203: | ||
V_{\rm Media}\\ | V_{\rm Media}\\ | ||
V_{\rm Slurry}\\ | V_{\rm Slurry}\\ | ||
\ | {\rm LF}\text{ (v/v)}\\ | ||
\tau\text{ (min)}\\ | \tau\text{ (min)}\\ | ||
\text{R/D* factor (frac)}\\ | \text{R/D* factor (frac)}\\ | ||
f_{\rm Ds}\text{ (-)}\\ | |||
f_{\rm Hb}\text{ (-)}\\ | |||
f_{\rm Ns}\text{ (-)}\\ | |||
f_{\rm S}\text{ (-)}\\ | |||
f_{\rm T}\text{ (-)}\\ | |||
f_{\rm Db}\text{ (-)}\\ | |||
f_{\rm WI}\text{ (-)}\\ | |||
\text{Iterations}\\ | \text{Iterations}\\ | ||
dt\text{ (s)}\\ | dt\text{ (s)}\\ | ||
| Line 319: | Line 331: | ||
where: | where: | ||
* <math>\ | * <math>{\rm LF}</math> is the media load fraction (v/v), defined as the fraction of mill volume occupied by media, including void spaces, i.e. <math>{\rm LF} = H_{\rm b} \big/ H</math> | ||
* <math>\text{R/D* factor}=D_i^*/D_i</math> is the discharge rate scaling factor | * <math>\text{R/D* factor}=D_i^*/D_i</math> is the discharge rate scaling factor | ||
* <math>Q_{\rm M,P}</math> is the mass flow rate of particles in the mill product (t/h) | * <math>Q_{\rm M,P}</math> is the mass flow rate of particles in the mill product (t/h) | ||
| Line 353: | Line 365: | ||
The SysCAD interface for Dynamic mode is described below. For steady-state, see ''[[Stirred Mill (Perfect Mixing)]]''. | The SysCAD interface for Dynamic mode is described below. For steady-state, see ''[[Stirred Mill (Perfect Mixing)]]''. | ||
{{SysCAD (Page, Mill, DLL*Mill)| | {{SysCAD (Page, Mill, DLL*Mill)|PowerModels=true|MediaStrings=true}} | ||
{{SysCAD (Page, Stirred Mill, Perfect Mixing, Mill)|method=1}} | {{SysCAD (Page, Stirred Mill, Perfect Mixing, Mill)|method=1}} | ||
{{SysCAD (Page, Ball Mill, Perfect Mixing, Ore)|method= | {{SysCAD (Page, Ball Mill, Perfect Mixing, Ore)|method=Stirred}} | ||
{{SysCAD (Page, Stirred Mill, Perfect Mixing, Ri/Di)|method=1}} | {{SysCAD (Page, Stirred Mill, Perfect Mixing, Ri/Di)|method=1}} | ||
| Line 365: | Line 377: | ||
{{SysCAD (Page, Ball Mill, Perfect Mixing, Content)}} | {{SysCAD (Page, Ball Mill, Perfect Mixing, Content)}} | ||
{{SysCAD (Page, | {{SysCAD (Page, Tumbling Mill, Power)|modelpage={{SysCAD (Text, UnitType Prefix)}}Mill|Nitta=true}} | ||
{{SysCAD (Page, Tumbling Mill, MediaStrings)|modelpage={{ | {{SysCAD (Page, Tumbling Mill, MediaStrings)|modelpage={{SysCAD (Text, UnitType Prefix)}}Mill}} | ||
{{SysCAD (Page, About)}} | {{SysCAD (Page, About)}} | ||
| Line 375: | Line 387: | ||
* [[Stirred Mill (Perfect Mixing)|Steady-state Perfect Mixing stirred mill model]] | * [[Stirred Mill (Perfect Mixing)|Steady-state Perfect Mixing stirred mill model]] | ||
* [[Mill (Herbst-Fuerstenau)| Herbst-Fuerstenau mill model]] | * [[Mill (Herbst-Fuerstenau)| Herbst-Fuerstenau mill model]] | ||
* [[Stirred Mill (Power, Nitta)]] | |||
* [[Stirred Mill (Power, Heath)]] | |||
== References == | == References == | ||
Latest revision as of 14:20, 3 July 2024
Description
This article describes a dynamic implementation of the Perfect Mixing vertical stirred mill model outlined by Napier-Munn et al. (1996).[1]
The dynamic version uses the same underlying theory and structure as the steady-state Perfect Mixing stirred mill model. For a full description of the steady-state model, see Stirred Mill (Perfect Mixing).
Model theory
The dynamic Perfect Mixing model is based on a population balance of particles entering the mill, breaking into smaller sizes, and discharging as product. For a mill operating in unsteady-state, the diagram in Figure 1 below represents the balance for a given size fraction:
The dynamic population balance is described mathematically as:[2]
where:
- is the index of the size interval, , is the number of size intervals
- is the mass feed rate of solids in size interval
- is the mass product rate of solids in size interval
- is the mass of solids in the mill load in size interval
- is the breakage rate of solids in the mill load in size interval
- is the rate of discharge from the mill of solids in size interval
- is the Appearance function, the distribution of particle mass arising from the breakage of a parent particle in size interval into progeny of size interval
Unlike the steady-state version, the load component cannot be eliminated from the equation, nor can the and components be combined into a single term. Therefore, the breakage and discharge rates and must be specified separately as inputs to the dynamic model.
Finally, an unsteady-state mill simulation must also consider the retention of liquids in the load:
where:
- is the load mass of water in the mill
- is the mass feed rate of water into the mill
- is the discharge rate of water from the mill, normally assumed to equal the value of at the finest size interval.
Time step discretisation
The unsteady-state Perfect Mixing differential equation is numerically solved by a discretised time stepping approach (i.e. Euler's method). The change in load mass in a size fraction during a sufficiently small time increment is:
Similarly, for liquids:
The time stepping approach is a convenient numerical approximation to the solution of the unsteady-state Perfect Mixing population balance differential equation. The approach is, however, subject to several limitations:
- The mass of particles separately discharged from or broken out of a size interval in a time step cannot exceed the mass of particles actually present in that size interval.
- Similarly, the overall maximum discharge flow rate of pulp from the mill cannot exceed the total volume of pulp in the mill in a time step.
The time step size used internally by the model is automatically reduced to ensure the breakage, discharge and pulp flow rate limits per step are not exceeded. This is achieved by computing a number of sequential sub-steps at the reduced internal step size for each requested external step.
This is useful if the either a fixed time step specified by an application is too large (e.g. SysCAD) or a numerical solution is desired in as few steps as possible (e.g. Excel). The automatic time step adjustment is largely invisible to the user and manifests only as a slightly slower execution speed.
The calculated time step size may be overridden with a larger user-specified sub-step count if increased accuracy in the numerical approximation is desired.
Breakage rate
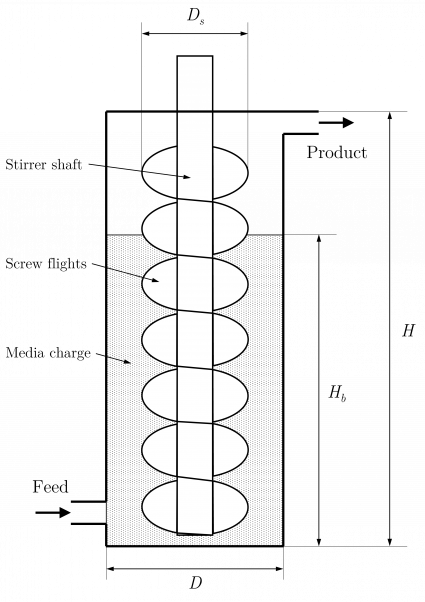
The breakage function, , is an input parameter for the dynamic Perfect Mixing model, replacing the term appearing in the steady-state version.
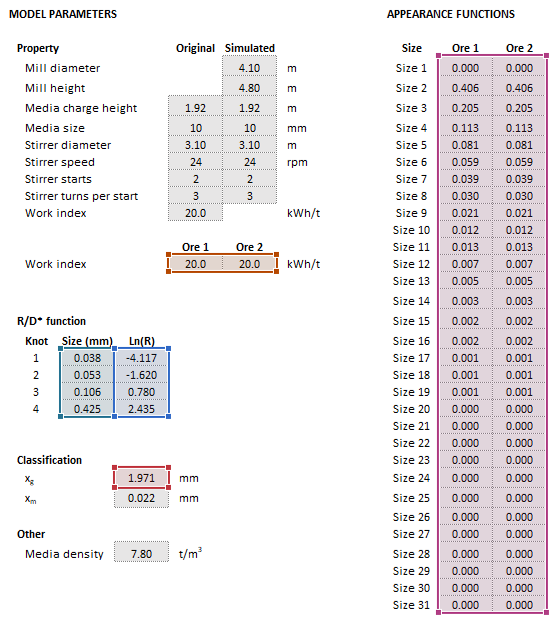
The breakage rate, , is affected by mill operating conditions as follows:
- is the stirrer diameter (m)
- is the stirrer speed (rpm)
- is the number of starts of the screw stirrer
- is the number of turns per start along the full height of the screw stirrer ()
- is the mean media diameter (mm)
Adopting the same scaling approach and nomenclature as the Perfect Mixing ball mill, the rate is scaled by the following relation:
The scaling factors are defined as:
where:
- the subscript refers to the original mill from which was derived
- the subscript refers to the mill being simulated (scaled)
- are scaling exponents, , , and
The Work Index scaling factor, , is retained from the Perfect Mixing ball mill model, where is the Bond Ball Work Index value of the ore (kWh/t).
The model user may optionally change the values of to suit specific test work results or operating data.
The discharge rate scaling factor, , is excluded from the breakage rate scaling term and is dealt with separately within the model (see Slurry filling and discharge, below).
Discharge rate
The classical Leung definition of discharge rate of solids from a perfectly mixed mill is:[3]
where:
and:
- is the fraction of load presented to the mill discharge per unit of time (h-1)
- is the classification function, the fraction of particles of size reporting to the mill product (frac)
- is the geometric mean size of particles in size interval (mm)
- is the particle size below which all mass in the size interval reports to mill product (mm), i.e. like water
- is the largest particle size which can report to mill product (mm)
Prior work suggests that internal classification within stirred mills may be represented by a Whiten efficiency curve (Hasan et al., 2016).[4] Leung's equation is likely to be an adequate approximation of the same classification behaviour.
Appearance function
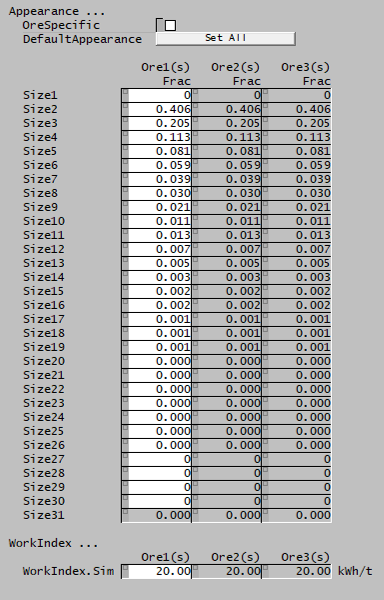
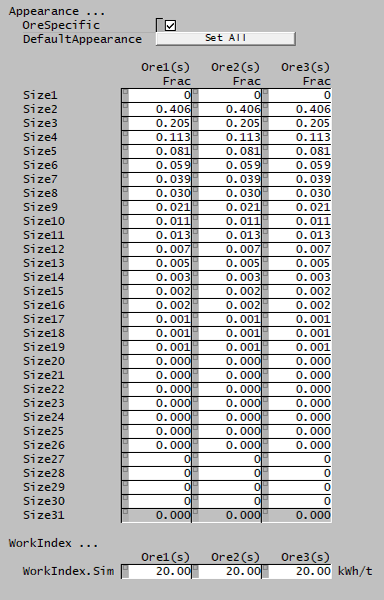
The Appearance function describes the mass-by-size distribution of progeny particles resulting from the breakage of parent particles.
The Appearance function may be specified for a particular ore.
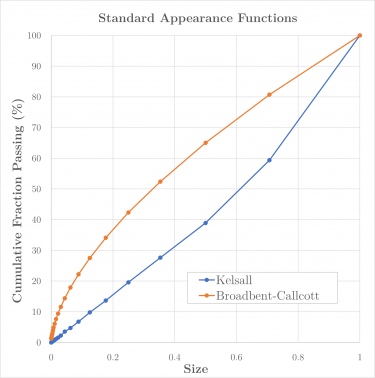
Morrell et al. (1993) found the appearance functions generated for the Perfect Mixing ball mill model were too fine for stirred mills. They recommended either generating new appearance functions at one-tenth of the standard breakage test input energy level, or using the Kelsall breakage function.[5]
Internal mesh series
The Perfect Mixing mill model is formulated internally with a geometric progression of 31 mesh sizes at intervals. Feed and product size fractions are automatically converted to and from the internal mesh series during model computation. The size intervals allow the appearance function to be specified as a one-dimensional matrix, rather than the two dimensional form defined above, since
when the intervals are so spaced.
Multi-component modelling
The original Perfect Mixing model formulation only considered the properties of a single ore type.
This implementation applies different appearance functions and breakage rate scaling factors to separate population balance computations for each ore type in the feed.
Slurry filling and discharge
The unsteady-state population balance and liquid hold-up models described above compute the quantity of slurry in the mill at each discrete time step.
Discharge flow does not commence from an initially empty stirred mill until the available internal volume is filled. The available internal volume consists of the grinding media interstices and any remaining space above the media charge.
The discharge rate, , whilst filling the mill is zero. During this period, the dynamic population balance reduces to a batch mill formulation (with or without feed), as outlined by Whiten (1974):[6]
Discharge commences once the internal mill volume is filled with slurry. The volumetric discharge rate of pulp from the mill is then, for practical purposes, equal to the instantaneous volumetric feed rate.
The model computes the value of to ensure the total flow rate of water plus solids classified for discharge matches the required product pulp outflow rate (i.e. the feed rate) for the mill.
Excel
The Perfect Mixing stirred mill model is not implemented in Excel in dynamic form for practical purposes. Excel is not an ideal platform for dynamic simulation and SysCAD (or similar) is preferred.
The dynamic model is, however, included in Excel in a run-to-steady-state mode where all feed and input parameters are fixed and time steps are progressed until the computed load and discharge stabilises.
This mode is useful for extracting separated and functions from steady-state data such as plant surveys or other model calibrations (including the steady-state Perfect Mixing stirred mill model).
The run-to-steady-state dynamic Perfect Mixing stirred mill model may be invoked from the Excel formula bar with the following function call:
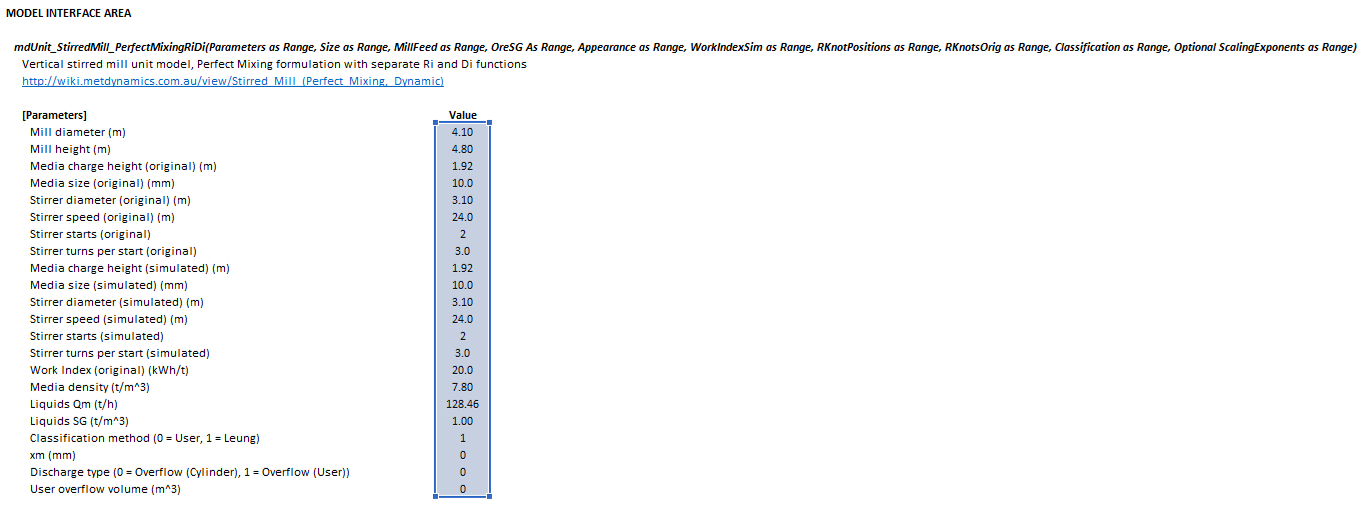
=mdUnit_StirredMill_PerfectMixingRiDi(Parameters as Range, Size as Range, MillFeed as Range, OreSG As Range, Appearance as Range, WorkIndexSim as Range, RKnotPositions as Range, RKnotsOrig as Range, Classification as Range, Optional ScalingExponents as Range)
Invoking the function with no arguments will print Help text associated with the model, including a link to this page.
Inputs
The required inputs are defined below in matrix notation with elements corresponding to cells in Excel row () x column () format:
where:
- is the mass flow feed rate of liquids into the mill (t/h)
- is the Specific Gravity or density of the media in the mill (- or t/m3)
- is the Specific Gravity or density of liquids in the feed (- or t/m3)
- is the number of ore types
- is the number of breakage rate per discharge rate knots
- is the size of the square mesh interval that feed mass is retained on (mm)
- , i.e. descending size order from top size () to sub mesh ( mm)
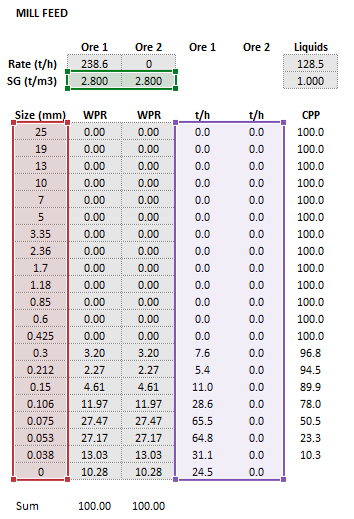
- is the mass flow rate of particles in the feed (t/h)
- is the Specific Gravity or density of solids (- or t/m3)
- is the method used to defined the classification-by-size to discharge, 0 = User-defined partition or 1 = Leung method
- is discharge configuration, 0 = Overflow discharge at mill height, 1 = Overflow discharge at user-defined slurry filling volume
- is the user-specified slurry filling volume at which overflow commences (if ) (m3)
- indicates the array is optional, the default values are used if omitted.
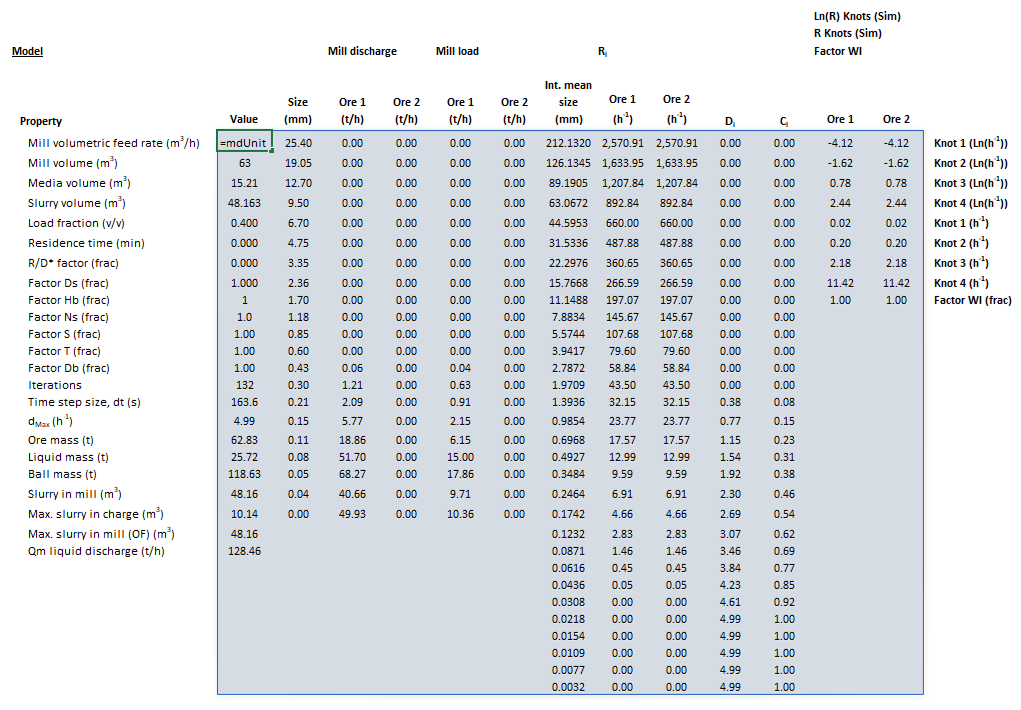
Results
The results are displayed in Excel as an array corresponding to the matrix notation below:
where:
- is the media load fraction (v/v), defined as the fraction of mill volume occupied by media, including void spaces, i.e.
- is the discharge rate scaling factor
- is the mass flow rate of particles in the mill product (t/h)
- is the geometric mean size of the internal mesh series interval that mass is retained on (mm)
- is the number of time steps required to reach steady-state
- is the size of the discretised time step calculated by the model, (s)
- is the total mass of ore in the mill at steady-state (t)
- is the mass of liquids in the mill at steady-state (t)
- is the mass of balls in the mill at steady-state (t)
- is the volume of slurry in the mill at steady-state (m3)
- is the maximum volume of slurry that can occupy the charge void space before (m3)
- is the maximum volume of slurry in the mill before overflow commences (m3)
- is the discharge mass flow rate of liquids from the mill (t/h)
- is the mass of solids in the mill (t)
Example
The images below show the selection of input arrays and output results in the Excel interface.
SysCAD
The SysCAD interface for Dynamic mode is described below. For steady-state, see Stirred Mill (Perfect Mixing).
MD_Mill page
The first tab page in the access window will have this name.
| Tag (Long/Short) | Input / Display | Description/Calculated Variables/Options |
|---|---|---|
| Tag | Display | This name tag may be modified with the change tag option. |
| Condition | Display | OK if no errors/warnings, otherwise lists errors/warnings. |
| ConditionCount | Display | The current number of errors/warnings. If condition is OK, returns 0. |
| GeneralDescription / GenDesc | Display | This is an automatically generated description for the unit. If the user has entered text in the 'EqpDesc' field on the Info tab (see below), this will be displayed here.
If this field is blank, then SysCAD will display the unit class ID. |
| Requirements | ||
| On | CheckBox | This enables the unit. If this box is not checked, then the material will pass straight through the mill with no change to the size distribution. |
| Method | Fixed Discharge | The discharge particle size distribution is user defined. Different distributions can be used for different solids. |
| AG/SAG (Variable Rates) | The Variable Rates AG/SAG mill model is used to determine the mill product size distribution. Different parameters can be used for different solids. | |
| Rod Mill (Lynch) | The Lynch rod mill model is used to determine the mill product size distribution. Different parameters can be used for different solids. | |
| Ball (Perfect Mixing) | The Perfect Mixing ball mill model (steady-state or dynamic) is used to determine the mill product size distribution. Different parameters can be used for different solids. | |
| Stirred (Perfect Mixing) | The Perfect Mixing stirred mill model (steady-state or dynamic) is used to determine the mill product size distribution. Different parameters can be used for different solids. | |
| Mill (Herbst-Fuerstenau) | The Herbst-Fuerstenau model is used to determine the mill product size distribution. Different parameters can be used for different solids. | |
| PowerModels | CheckBox | Show alternative mill power model calculations on the Power page. |
| MediaStrings | CheckBox | Show media size distributions at recharge equilibrium on the MediaStrings page. |
| Options | ||
| ShowQFeed | CheckBox | QFeed and associated tab pages (eg Sp) will become visible, showing the properties of the combined feed stream. |
| ShowQProd | CheckBox | QProd and associated tab pages (eg Sp) will become visible, showing the properties of the products. |
| SizeForPassingFracCalc | Input | Size fraction for % Passing calculation. The size fraction input here will be shown in the Stream Summary section. |
| FracForPassingSizeCalc | Input | Fraction passing for Size calculation. The fraction input here will be shown in the Stream Summary section. |
| Stream Summary | ||
| MassFlow / Qm | Display | The total mass flow in each stream. |
| SolidMassFlow / SQm | Display | The Solids mass flow in each stream. |
| LiquidMassFlow / LQm | Display | The Liquid mass flow in each stream. |
| VolFlow / Qv | Display | The total Volume flow in each stream. |
| Temperature / T | Display | The Temperature of each stream. |
| Density / Rho | Display | The Density of each stream. |
| SolidFrac / Sf | Display | The Solid Fraction in each stream. |
| LiquidFrac / Lf | Display | The Liquid Fraction in each stream. |
| Passing | Display | The mass fraction passing the user-specified size (in the field SizeForPassingFracCalc) in each stream. |
| Passes | Display | The user-specified (in the field FracForPassesSizeCalc) fraction of material in each stream will pass this size fraction. |
Mill page
The Mill page is used to specify the input parameters for the mill model.
| Tag (Long/Short) | Input / Display | Description/Calculated Variables/Options |
|---|---|---|
| PerfectMixing | ||
| HelpLink | Opens a link to this page using the system default web browser. Note: Internet access is required. | |
| Requirements | ||
| NumParallelUnits | Input | The number of parallel, identical units to simulate:
|
| Mode | Steady State |
|
| Dynamic | The dynamic Perfect Mixing stirred mill model described here is used to determine the mill product size distribution. Different parameters can be used for different solids. | |
| MinSubSteps | Input | The user-specified minimum number of internal models steps taken per SysCAD step. |
| SubSteps | Display | The actual number of internal models steps taken per SysCAD step. May be affected by breakage/discharge rates or the user-specified MinSubSteps parameter. |
| DischargeType | Overflow | The maximum slurry volume in the mill before overflowing is calculated by the model. |
| Overflow (User) | The maximum slurry volume in the mill before overflowing is specified by the user. | |
| MediaStringsP50 | CheckBox |
|
| Stirred | ||
| UserExponents | Checkbox | Indicates whether to use user-defined values for the scaling exponents. |
| MillDiameter | Input | The inside liner diameter of the simulated mill. |
| MillHeight | Input | The height of the simulated mill. |
| MediaHeight | Input | Height of the media charge of the original and simulated mills. |
| MediaDiameter | Input | Median diameter of the media in the original and simulated mills. |
| StirrerDiameter | Input | Diameter of the stirrers of the original and simulated mills. |
| StirrerSpeed | Input | Rotational speed of the stirrers of the original and simulated mills. |
| StirrerStarts | Input | Number of starts of the (screw) stirrers of the original and simulated mills. |
| StirrerTurns | Input | Number of turns per start of the (screw) stirrers of the original and simulated mills. |
| WorkIndex | Input | Bond Ball Work Index of ore in the original mill. |
| Exponent | Input |
|
| RFunction | ||
| NumSplineKnots | Input | Number of spline knots for the function. |
| Size | Input | Spline knot size positions. |
| Ln(R) | Input | Values of at each spline knot position. |
| Results | ||
| MillVolume | Display | Volume inside the mill. |
| MediaVolume | Display | Volume occupied by the media in the mill, excluding void space. |
| SlurryVolume | Display | Volume of slurry in the mill, including slurry in media void space and above media charge. |
| LoadFraction | Display | Volume of media charge, including void space and excluding stirrer volume, as a fraction of mill volume, excluding stirrer volume. |
| ResidenceTime | Display | Mean residence time of slurry in the mill. |
Ore page
This page is used to define the comminution properties of SysCAD species with the size distribution quality in the project.
| Tag (Long/Short) | Input / Display | Description/Calculated Variables/Options |
|---|---|---|
| Appearance | ||
| DefaultAppearance | Sets all species to the the default Kelsall Appearance function. | |
| OreSpecific | CheckBox |
|
| Appearance | Input | User-specified Appearance function data for all species with size distribution property. |
| WorkIndex | ||
| WorkIndex.Sim | Input | Bond Ball Work Index data for all species with size distribution property. |
RiDi page
This page displays the scaling factors and breakage rate per discharge rate for each size interval computed by the Perfect Mixing model.
| Tag (Long/Short) | Input / Display | Description/Calculated Variables/Options |
|---|---|---|
| Scaling | ||
| StirrerDiameter | Display | Value of the stirrer diameter factor for rate scaling. |
| MediaHeight | Display | Value of the media height factor for rate scaling. |
| StirrerSpeed | Display | Value of the stirrer speed factor for rate scaling. |
| StirrerStarts | Display | Value of the stirrer starts factor for rate scaling. |
| StirrerTurns | Display | Value of the stirrer turns per start factor for rate scaling. |
| MediaSize | Display | Value of the media size factor for rate scaling. |
| WorkIndex | Display | Value of the Work Index factor of each ore species for rate scaling. |
| Rates | ||
| Size | Display | Size of each interval in internal mesh series. |
| MeanSize | Display | Geometric mean size of each interval in internal mesh series. |
| R | Display | Value of breakage rate, , for each size interval, for each ore species. |
| C | Display | Value of classification function, , for each size interval. |
| D | Display | Value of discharge rate, , for each size interval. |
Load page
This page displays information about the balls, solids and liquids that currently comprise the mill load.
| Tag (Long/Short) | Input / Display | Description/Calculated Variables/Options |
|---|---|---|
| Filling | ||
| SLCapacity / SLVtCap | Input / Display | The maximum volume of slurry the mill can contain before overflow. |
| SLCharge / SLVtCharge | Display | Only appears if DischargeType is 'Overflow'. The maximum volume of slurry that can fill the charge void space. |
| SLVolume / SLVt | Display | The total volume of slurry currently in the mill. |
| SLLevel / SLLvl | Display | The current slurry volume (SLVolume) as a fraction of the maximum slurry volume before overflow (SLCapacity). |
| Load | ||
| SolidMass / SMt | Display | The mass of solids with the SysCAD size distribution property currently in the mill. |
| LiquidMass / LMt | Display | The mass of liquids plus solids without the SysCAD size distribution property currently in the mill. |
| BallMass / BMt | Display | The mass of ball media in the mill. |
| Size | Display | Size of each interval in internal mesh series. |
| MeanSize | Display | Geometric mean size of each interval in internal mesh series. |
| Load | Display | The mass of solids with the SysCAD size distribution property currently in the mill, by size and species. |
Content, Sp, Ec, Sz and MSz pages
These pages display the standard SysCAD Material Content, Species Content and Size pages for the current mill load
Power page
This optional page displays the inputs and results for alternative mill power models. The page is only visible if PowerModels is selected on the MD_Mill page.
| Tag (Long/Short) | Input / Display | Description/Calculated Variables/Options |
|---|---|---|
| Power | ||
| Nitta | CheckBox | Shows inputs and results for stirred mill power calculations using the Nitta method. |
| Heath | CheckBox | Shows inputs and results for stirred mill power calculations using the Heath method. |
MediaStrings page
This page displays the inputs and results for grinding mill media string calculations. The page is only visible if MediaStrings is selected on the MD_Mill page.
About page
This page is provides product and licensing information about the Met Dynamics Models SysCAD Add-On.
| Tag (Long/Short) | Input / Display | Description/Calculated Variables/Options |
|---|---|---|
| About | ||
| HelpLink | Opens a link to the Installation and Licensing page using the system default web browser. Note: Internet access is required. | |
| Information | Copies Product and License information to the Windows clipboard. | |
| Product | ||
| Name | Display | Met Dynamics software product name |
| Version | Display | Met Dynamics software product version number. |
| BuildDate | Display | Build date and time of the Met Dynamics Models SysCAD Add-On. |
| License | ||
| File | This is used to locate a Met Dynamics software license file. | |
| Location | Display | Type of Met Dynamics software license or file name and path of license file. |
| SiteCode | Display | Unique machine identifier for license authorisation. |
| ReqdAuth | Display | Authorisation level required, MD-SysCAD Full or MD-SysCAD Runtime. |
| Status | Display | License status, LICENSE_OK indicates a valid license, other messages report licensing errors. |
| IssuedTo | Display | Only visible if Met Dynamics license file is used. Name of organisation/seat the license is authorised to. |
| ExpiryDate | Display | Only visible if Met Dynamics license file is used. License expiry date. |
| DaysLeft | Display | Only visible if Met Dynamics license file is used. Days left before the license expires. |
See also
- Steady-state Perfect Mixing stirred mill model
- Herbst-Fuerstenau mill model
- Stirred Mill (Power, Nitta)
- Stirred Mill (Power, Heath)
References
- ↑ 1.0 1.1 Napier-Munn, T.J., Morrell, S., Morrison, R.D. and Kojovic, T., 1996. Mineral comminution circuits: their operation and optimisation. Julius Kruttschnitt Mineral Research Centre, Indooroopilly, QLD.
- ↑ Valery Jnr, W. and Morrell, S., 1995. The development of a dynamic model for autogenous and semi-autogenous grinding. Minerals engineering, 8(11), pp.1285-1297.
- ↑ Leung, K., Morrison, R.D. and Whiten, W.J., 1987. An Energy Based Ore Specific Model for Autogenous and Semi-autogenous Grinding, Copper 87, Vina del Mar, Vol. 2, pp 71 - 86
- ↑ Hasan, M., Palaniandy, S., Hilden, M. and Powell, M., 2016. Investigating internal classification within gravity induced stirred mills. Minerals Engineering, 95, pp.5-13.
- ↑ 5.0 5.1 Morrell, S., Sterns, U.J. and Weller, K.R., 1993. The application of population balance models to very fine grinding in tower mills. 18th International Mineral Processing Congress; 23-28 May, 1993; Sydney, NSW. 1993, pp. 61-66.
- ↑ Whiten, W.J., 1974. A matrix theory of comminution machines. Chemical Engineering Science, 29(2), pp.589-599.